√99以上 等比数列 一般項 公式 127395

等差数列（一般項） 1631 3．等差数列（和） 941 4．等比数列（一般項） 1731 5．等比数列（和） 1044 6．等比数列の和の公式の使用例 748 7．ジグザグ型の数列 537 8．調和数列 215 9．シグマの意味 1245 10．シグマの公式 849 11．階差数列（一般項等比数列の一般項は，植木算の関係で になりますが 等比数列の和()は ではありません．上記の中間項を消す解説図をよく見ると，末項（第 n 項） ar n−1 は消えて，代わりにそれに r を掛けた ar n が残ることが分かります． だから，正しいのは 等比数列の和を求める公式 等比数列の初項からある項までをすべて足し合わせる公式がある。 初項a、公比r、項数nの等比数列の和S n を求める公式は以下。 等比数列の公式の証明は応用的な内容なので、余裕がある方は確認していただきたい。

等比数列公式总结 信息图文欣赏 信息村 K0w0m Com

等比数列 一般項 公式

等比数列 一般項 公式-等比数列型の漸化式を用いる前にまずは等比数列の一般項の公式を思い出しておきましょう。 等比数列の一般項は で求めることができました。 漸化式では初項と公比を求めることができ、それを用いて基本の等比数列の一般項の公式を解くことで一般項を求めることができます。次の数列の一般項を求めよ。 a 1 ＝1, a n1 ＝2a n －3 考え方 この数列は、等差数列でも等比数列でもない。 式もよくわからないので、 その他（漸化式）を用いて一般項を求める。（階差数列でも解

级数求和公式等比数列求和公式 学习岛

N = 1 n=1 n = 1 の場合を分けて考える必要があります。 ただし，高校数学，大学入試で登場するほとんど全ての問題では n ≥ 2 n\geq 2 n ≥ 2 の場合の結果が n = 1 n=1 n = 1 の場合にも正しいので，場合分けの必要性を実感しにくいです。 しかし，うまくいか等比数列（とうさすうれつ）の一般項は「ar (n－1) 」で算定します。aは初項、rは公比、nは第n項のことです。 aは初項、rは公比、nは第n項のことです。等差数列の和 や 等比数列の和 の公式で見てきたように、数列の和は、初項、交差、公比、といった一般項を決定するための条件を用いることによって求めることができました。 ここではそれとは逆に、数列の和から一般項を

 等比数列の一般項 等比数列の一般項を表す式 最初に 等比数列の一般項を表す式 を紹介します。 一般項とは数列{\(a_n\)}の第n番目の項をnを用いて表すことです。 一般項を求めれば、nに特定の値を代入するだけで数列の各項を求めることができます。 等比数列の一般項 一般項とは数列の第 番目が何になるかを意味するものです。 先の例の数列を とおくと、 であり、 から までを書き下すと、 となりますが、ここで が であるのは、 に対し、交比である を1回かけたからです。 同様に、 は交比を2回、 は交比を3回かけたものになりま 等比数列の一般項の公式を覚えるには、一般項の成り立ちを理解するのが一番です。 初項 \(a\)、公比 \(r\) の等比数列 \(\{a_n\}\) は以下のように表せます。

從等比數列的一般項可知，任意一個可以寫成 a n = p q n {\displaystyle a_{n}=pq^{n}} 形式的數列，都是一個等比數列，其中公比 r = q {\displaystyle r=q} ，首項 a = p q {\displaystyle a=pq} 。Σの公式 ∑ k = 1 n α = n α ∑ k = 1 n k = 1 2 n ( n 1) ∑ k = 1 n k 2 = 1 6 n ( n 1) ( 2 n 1) ∑ k = 1 n k 3 = { 1 2 n ( n 1) } 2 ∑ k = 1 n r k = r ( 1 − r n) 1 − r ( r ≠ 1)幾何数列）は、隣り合う二項の比が項番号によらず等しい数列を言う。 各項に共通する (common) その一定の比のことを公比（こうひ、英 common ratio ）という。 例えば 4, 12, 36, 108, という数列 (a n) ∞ n=1 は、各項が直前の項に 3

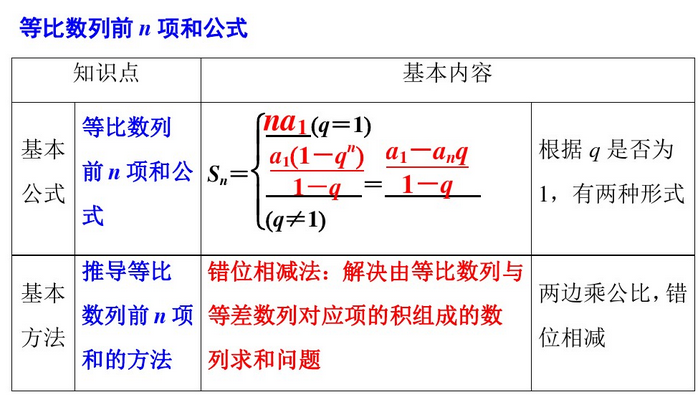
数列前n项和公式 早做准备

等比数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

初等数学公式集/数列 出典 フリー教科書『ウィキブックス（Wikibooks）』 < 初等数学公式集 ナビゲーションに移動 検索に移動 目次 1 一般項;等比数列の一般項 (基本) an = a1 ⋅rn−1 a n = a 1 ⋅ r n − 1 しかし， an a n を求めるために，わざわざ a1 a 1 から掛けねばならない理由はありません．MathAquarium定理・公式の証明数列の公式 1 1 等差数列 等差数列{a n}の初項をa，公差をd，末項をl，一般項をa n，初項から第n 項までの和をS n とすると a n＝a＋(n－1)d， S n＝ 2 1 n(a＋l)＝ 2 1 n{2a＋(n－1)d} 2 等比数列 等比数列{a n}の初項をa，公比をr，一般項をa

等比数列通项公式求和怎么求 中国教育网

等比数列 维基百科 自由的百科全书

等比数列の和 32から33連勝します！ 個人投資家にとって等比数列の和は重要公式の一つですね！ たいへん重宝しています。 k=のバージョンも作ってほしい。 大学の宿題にとても助かりました。 アンケートにご協力頂き有り難うございました。 送信を等比数列の一般項を求める公式 $$a_n=ar^{n1}$$ $$a初項 r公比$$ 等比中項 3つの項の等比数列\(a, b, c\)について、次の式が成り立つ。 $$b^2=ac$$ 等比数列の和を求める公式 \(r\neq 1\) のとき $$S_n=\frac{a(1r^n)}{1r}=\frac{a(r^n1)}{r1}$$ \(r=1\) のとき $$S_n=na$$等比数列の一般項の公式に加えて、階差数列型の一般項の公式や等比数列の総和の公式も使う手強い問題ですね。 \(q^n\) で割る \(a_{n1}=pa_nq^n\) の形のときは 両辺を \(q^n\) で割って 等差数列の一般項や和の公式をマスターしよう！ ますますmath

等比数列求和公式推导 万图壁纸网

关于高中数学 求数列前n项和的问题 掌握这7种方法 考试不再难 知乎

MathAquarium例題数列 3 2 等差中項・等比中項 4 つの数1，a，b，10 がある。1，a，b はこの順で等比数列をなし，a，b，10 はこの順で等差数列をなす。 このような実数a，b をすべて求めよ。 ・等差中項 数列a，b，c が等差数列のとき，b をa とc の等差中項といい， 2b＝a＋c が成り立つ。 2 等差数列とは？ 21 等差数列とは「はじめの数に、一定の数を足し続ける数列」 22 等比数列と何がちがう？ 3 等差数列の公式の意味を説明！ 31 「初項」「公差」だけを押さえれば等差数列の一般項は求められる 32 等差数列のコツ：両脇を足したら2 数列 となり、これは等比数列なので、一般項

等比数列前n项和公式是什么如何运用 有途教育

1

等差数列 $\{a_{n}\}$ で第 $17$ 項が $132$，第 $29$ 項が $54$ のとき，この数列の一般項を求めよ． 練習2 等差数列 $\{a_{n}\}$ で第 $12$ 項が $69$，第 $$ 項が $53$ のとき，この数列の和の最数列通项公式概念 不妨将数列递推公式中同时含有a n 和a n1 的情况称为一阶数列，显然，等差数列的递推式为 a n =a n1 d , 而等比数列的递推式为 a n =a n1 * q ； 这二者可看作是一阶数列的特例。 故可定义一阶 递归数列 形式为： a n1 = A *a n B等差数列・等比数列・階差数列の意味と一般項を求める公式 Tooda Yuuto 18年11月19日 / 19年9月9日 社会・経済・自然科学において「 ある時点での値が、それより前の時点での値をベースに決まる もの」は少なくありません。

等比数列公式等比数列公式 尚书坊

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

等比数列の和の公式は $r \ne 1$のとき $Sn = {a(1 r^n) \over 1 r}$ r = 1の時、 $Sn = na$ となります。 等比数列の和とは、『 初項a、公比rの等比数列の初項から第n項までの和 』を意味しています。 具体的な例を見てみましょう。 先ほど紹介した等比数列の初項から第\(4\)項までの合計を計算してみます。 等比数列の一般項の公式 初項\( a_1 \)、公比\( r \)の等比数列\( \{ a_n \} \)の一般項\( a_n \)は、 \begin{align*} a_n = a_1 \cdot r^{n1} \\ \end{align*} と表すことができる。

等比数列の一般項と和 おいしい数学

级数求和公式等比数列求和公式 学习岛

等比×等差の和を求める2通りの方法 は2通りの方法で計算できる。 p=1 p = 1 の場合が超頻出です。 p=2 p = 2 の場合もまれに出ます。 p\geq 3 p ≥ 3 の場合は計算量が非常に多くなってしまい実際に計算する機会はほぼありませんが，「（p乗)× (等比)の和は原理Start studying 数列公式集 Learn vocabulary, terms, and more with flashcards, games, and other study toolsこのように階差数列の一般項が簡単に表せる場合には、 n≧2 のとき a_n=a_1\displaystyle \sum_ { k = 1 }^ { n1 } b_k こちらの公式に当てはめて、一般項を求めていきましょう。 ただし、先ほどの章でも言いましたが、 こちらの公式が使えるのは、 n≧2 のときだけ

数学核心考点秒杀 等差数列 等比数列学习技巧大放送 收藏 知乎

51好课 课程介绍 等比数列的概念 通项公式

等比数列（とうひすうれつ、英 geometric progression, geometric sequence;数学II数列について質問です。 この問題の答えの三項間を解いてるところで等比数列の一般項の公式を使っています。 普通の公式は An=初項•(公比)のn1乗 なのに対してここでは An=初項•(公比)n乗 を使っています。 なぜでしょうか？

数列 从错位相减到阿贝尔变换 知乎

高考数学考点之数列的综合应用 王羽课堂

等比数列中项公式 100查分网

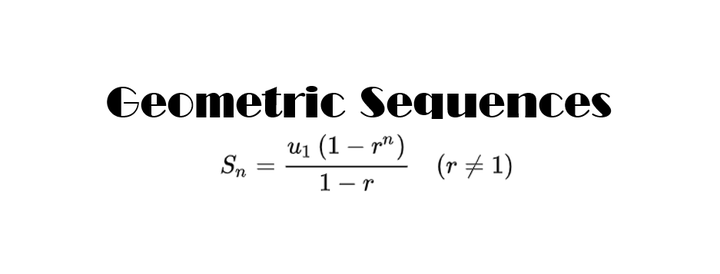
数 你好看 等比数列 Geometric Sequences 知乎

等比数列前n项和公式的一个变形式及其推论 知乎

等比数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

利用等比数列求和 图片欣赏中心 急不急图文 Jpjww Com

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

等比数列公比的公式是什么 公比是什么意思 30高考网

高中数学 等差 等比数列混合题 常规题型更要熟练掌握 公式

高中数学 数列综合题 证明等比数列 常考题必须掌握 An

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

要点梳理1 等比数列的定义如果一个数列 那么这个数列叫做等比数列 这个常数叫做等比数列的 通常用字母表示 2 等比数列的通项公式

3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

级数求和公式等比数列求和公式 学习岛

江苏省清江中学高中数学16等比数列的概念与通项公式教学案苏教版必修5下载 Word模板 爱问共享资料

等比数列求和公式 互动百科 Math Equations Math Equation

等比中項 數列問題中的特殊性質 如果在等比數列a項和b項中 插入一個數g 百科知識中文網

高考数学 数列求和的常用方法 知乎

高中数学 由数列相邻两项间的递推关系求通项 还不会快来学 公式

21届高考数学一轮复习第六章数列第3节等比数列及其前n项和教学案 含解析 莲山课件

高中数学 数列求和方法集锦 含经典例题及解析 转需 知乎

数列と級数 Of 京極一樹の数学塾会員頁

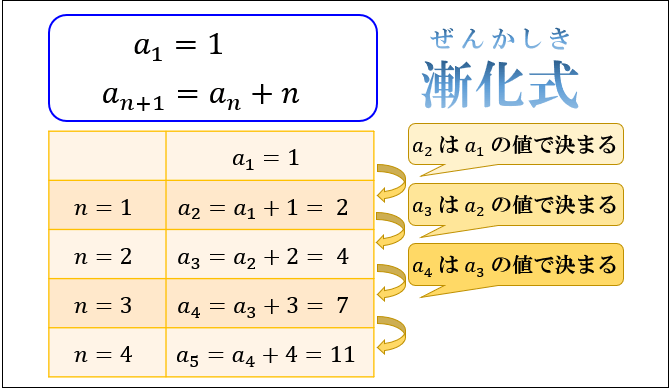
漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

09 等比中项等比数列高中数学 Youtube

等比数列的定义及通项公式 百度文库

行测如何巧用公式解等差等比数列 新闻频道 手机搜狐

3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ

等比数列前n项和公式和等比数列前n项和公式 师乐教师招聘考试答疑 师乐师考教师网

数列 等比数列 1 通项公式与性质 哔哩哔哩 つロ干杯 Bilibili

奇妙的a Level数列 你了解透彻了吗 A加未来国际教育

等比数列 等差数列 简书

等差等比数列公式汇总 搜狗图片搜索

等比数列 维基百科 自由的百科全书

高中数学必修5 构造等比数列求通项公式 基础 方法步骤 哔哩哔哩 つロ干杯 Bilibili

等比数列求和公式 快懂百科

等差数列公式图 等差数列等比数列前n项和公式总结 学习岛

行测如何巧用公式解等差等比数列

必修五 高中数学必备知识点 26 等比数列通项公式跟踪训练 练习题

数列的通项公式求法有哪些 高三网

等比数列前n项和公式是什么 等比数列性质 30高考网

高中数学 数列综合题 证明等比数列 常考题必须掌握 An

While End循环结构求等比数列的和 百度经验

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

等比数列概念及通项公式 哔哩哔哩 つロ干杯 Bilibili

等比数列概念与通项公式 学习视频教程 腾讯课堂

等比数列通项公式两种 扒拉扒拉

等比数列求和公式等差等比数列求和公式 爱华网

等比数列求an 等比数列求an通项公式 等比数列的所有公式

3 2 等比数列的前n项和 一 每日头条

等比数列前n项和的公式 高三网

等比数列の一般項と和 おいしい数学

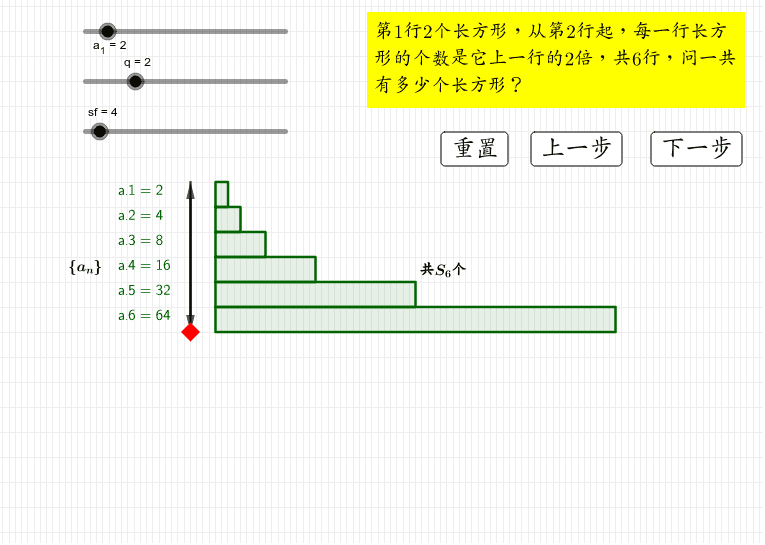
等比数列前n项和公式 Geogebra

03 应用等比数列求和公式求项或公比等比数列的前n项和高中数学 Youtube

等比数列 一般項や和の計算 数学の偏差値を上げて合格を目指す

等比数列 Ppt Download

等比数列とは 一般項や等比数列の和の公式 シグマの計算問題 受験辞典

等比数列含义及通项公式 公开课教学ppt课件 Ppt 教育文库 教育资源网 新时代文库www Xsdwk Com 教育文库 教育资源网 新时代文库www Xsdwk Com

等比数列的通项公式 教案 下载 Word模板 爱问共享资料

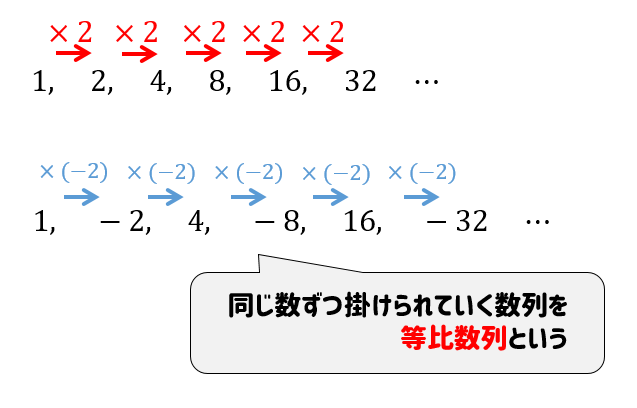
等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

第二章数列2 4等比数列2 4 1等比数列的概念及通项公式 教案 新人教a版必修5 Doc 课件巴巴kejian Com 课件巴巴kejian Com

等比数列公式总结 信息图文欣赏 信息村 K0w0m Com

高中數學 等比數列的概念和運用 通項公式和前n項和的綜合 每日頭條

等比数列の一般項と和 おいしい数学

1

48s96ub7b0z5f Net Touhisuuretsu

高校数学b 等比数列の一般項 A N Ar N 1 受験の月

等比数列求和公式 搜狗百科

等比数列前n项和公式是什么 高三网

等比数列

数列求通项公式等差等比判断和证明及求和 高中数学 教育 教育其他

等差公式等比公式數列 等差 等比數列求和公式 Prxbri

等比数列 高中数学知识点 高考圈

已知数列及等差数列若1证明数列为等比数列2求数列及数列的通项公式3设数列的前n项和为求 X题卡

等比数列的前n项和公式及推导过程 飞将高考

你应该想想 等比数列的求和是怎么来的 知乎

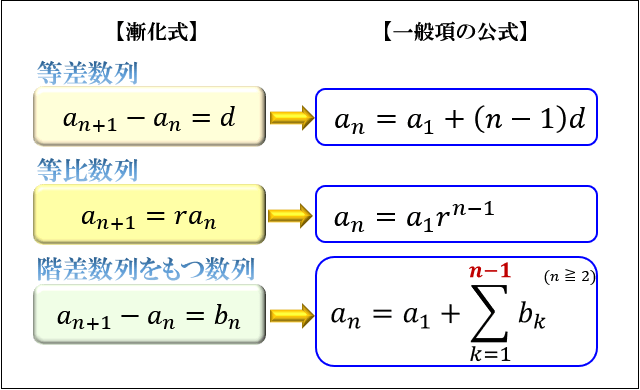
漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

等比数列求和公式等比数列求和公式常用算法 爱华网

苏教版数学高二年级必修5教案第2章数列第9课等比数列的概念和通项公式下载 Word模板 爱问共享资料

等比数列公式q怎么求 搜狗图片搜索

3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ

等比数列及它的和

等比数列 小学数学知识点

2 2 1 等比数列的概念和通项公式 Ppt Download

必修五 高中数学必备知识点 26 等比数列通项公式跟踪训练 练习题

高考数学 数列求和的常用方法 知乎

02 应用等比数列求和公式求和等比数列的前n项和高中数学 Youtube